코로나19 바이러스가 여전히 맹위를 떨치면서 전 세계적으로 고통과 혼란이 지속되고 있다. 특히 우리나라의 경우 하루 확진자 증가 폭이 100명 안팎을 오가면서 다소 줄어들기는 하였지만, 미국과 유럽 등지에서 감염자가 급증하고 있는 상황에서 외국으로부터의 유입을 차단하는 것이 새로운 고민거리가 되고 있다.

많은 사람들은 코로나19 바이러스의 유행이 언제쯤 종료될 수 있을 것인지, 또한 그 시점을 정확히 예측할 수 있을지 궁금해한다. 이와 관련해서 도움을 줄 수 있는 과학 분야가 바로 생물통계학(Biostatistics)과 복잡계 물리학 등이다.

오래전부터 지속적으로 전염병 발병하고 있어

현재의 코로나19 바이러스뿐만 아니라, 오래전부터 인류를 위협하거나 큰 피해를 끼친 전염병은 이어져 왔다. 흑사병이라고도 불리는 페스트가 중세 이후 유럽에서 가끔 대유행할 때에는 갑자기 인구의 3분의 1 이상이 줄어든 나라들도 있을 정도로 엄청난 희생자를 냈고, 신대륙 발견 이후 유럽인들이 이곳에 전파한 천연두 바이러스에 의해 원주민들은 거의 절멸할 정도가 되었다.

제1차 세계대전 직후인 1918년에 창궐한 스페인 독감은 전 세계적으로 사망자가 5000만 명 이상까지 이르렀을 것으로 추정되며, 20세기 후반 이후에도 가공할 치사율을 지닌 에볼라(Ebola) 바이러스, 에이즈(AIDS), 사스(SARS), 신종 플루 등이 지속적으로 인류를 괴롭혀왔다. 또한 생물학적인 감염병은 아니지만 컴퓨터 바이러스의 창궐 역시 순식간에 수많은 컴퓨터를 감염시키거나 인터넷망을 마비시키는 등 큰 피해를 끼쳐왔다.

수리과학적 모형에 기반 둔 예측 방법 다양

수리과학적 모형에 기반을 둔 전염 확산 연구의 역사는 무척 오래되었는데, 1766년에 스위스의 수학자 베르누이(Daniel Bernoulli, 1700-1782)가 천연두를 대상으로 처음 연구한 것으로 알려져 있다. 20세기 들어서 1927년부터 1933년까지 영국 왕립학회지에 3편에 걸쳐서 출판된 ‘A Contribution to the Mathematical Theory of Epidemic’이라는 제목의 논문이 현대적인 연구의 시작이다. 이 논문에서 연구자들은 전염병 확산의 기본이 되는 구획화(compartmental) 모델을 제시하는데, 이는 거의 백 년이 지난 오늘날까지도 유용하게 사용되는 체계이다.

즉 이 모델에 따르면 질병의 전염 상태를 아직 감염되지 않았지만 감염의 가능성이 있는 민감군 S(susceptible), 감염은 되었지만 발병하지 않은 잠복 상태인 노출군 E(exposed), 감염되어 다른 개체를 감염시킬 수 있는 전염군 I(infected), 질병이 회복되어 면역된 상태인 회복군 R(recoved)로 나누어 이들 군 사이의 상태 전이를 모형화한다. 전염병의 확산에 따라 S -> E -> I -> R의 단계로 진화하므로 이른바 SEIR 모델이라 부르는데, 간혹 잠복기의 노출군인 E의 상태를 제외하여 SIR 만으로 모델링 하기도 한다.

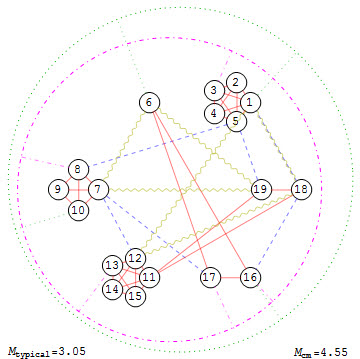
복잡계 네트워크 구조 고려해야

이와 같은 모델에 기반을 둔 전염병의 확산 연구는 전통적으로 수리생물학 또는 생물통계학의 영역이었으나, 근래 복잡계 물리학의 발전에 따라 복잡계 네트워크 이론 등이 이 분야의 연구에 큰 영향을 끼치고 있다.

즉 많은 질병이 개인 사이의 사회적 네트워크를 통하여 일어나므로, 복잡한 시스템에서 일어나는 전염 확산 현상을 제대로 이해하기 위해서는 이를 매개하는 복잡 네트워크의 구조 등에 대한 이해가 필요하기 때문이다.

꼭짓점(vertex)과 선분(edge)으로 이루어지는 복잡계 네트워크 모형에서는 각각의 구성 원소를 하나의 꼭짓점에 대응시키고, 상호작용을 하는 각 꼭짓점들을 선분(edge)으로 연결함으로써, 수많은 구성요소들이 복잡하게 상호작용을 교환하는 시스템에 대한 유용한 수학적 모델을 제공한다.

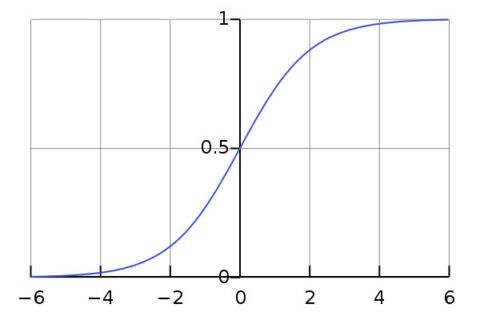
전염병 감염자의 수치 증가 등을 매우 단순화한 모델로는 이른바 로지스틱 곡선(logistic curve)이 많이 쓰인다. 벨기에의 수학자 베르휼스트가 1838년에 인구증가 과정을 설명하는 법칙으로서 제안한 이 S자형의 곡선은 이후 생물의 증식 현상이나 경제발전 과정 등을 근사적으로 모델링 하는 데에 자주 쓰여왔다. dN/dt=rN(1-(N/K)) 등과 같은 형태로서 시간(t)을 변수로 하여 확진자 수(N)가 변화하는 미분방정식을 따르게 된다.

섣부른 판단 조심해야

그러나 첨단의 연구기법을 적용하여 어떤 수학적 모델을 쓰든, 감염병의 종료 시점을 정확히 예측하기는 무척 어려운 일이다. 즉 상황이 모두 종료된 이후에는 수치적 모델을 적용하여 잘 설명할 수 있을지 몰라도, 전염병의 창궐이 한창 진행 중일 때에는 예상하지 못한 온갖 변수들이 갑자기 튀어나오기 일쑤이기 때문에, 현재까지 알려진 수치만으로 예측한 결과는 현실을 제대로 반영하기 힘들다.

저명한 통계 물리학자가 지난 2월 중순에 로지스틱 곡선 모델을 적용하여 국내에서 2월 말 또는 3월 초에 코로나19의 확산이 종료될 것이라고 조심스럽게 예측하였으나, 얼마 지나지 않아 특정 종교집단 등을 중심으로 감염자가 폭증하면서 본의 아니게 대중들과 방역 당국을 혼란스럽게 한 바 있다.

이후로도 3월 말 또는 6월 중순 등으로 코로나19의 국내 유행이 종료될 것이라는 예측과 연구 결과 등이 언론에 나온 바 있다. 그러나 관련 분야의 과학자들이 이러한 연구를 진행하는 것은 당연한 일이겠으나, 대중들에게 발표할 때에는 보다 신중을 기해야 한다.

감염병의 정확한 종료 시점과 최종 환자 수 등을 섣불리 예측하여 어긋난다면 도리어 과학에 대한 대중들의 불신이 커질 수 있기 때문이다.