“한 면이 9칸으로 나뉘고 면마다 색깔이 다른 정육면체를 이리저리 돌려 맞추는 퍼즐은?” 하는 질문을 던지면 누구든 금세 ‘루빅스 큐브(Rubik's Cube)’라고 답한다.

루빅스 큐브는 1974년 헝가리 발명가 에르노 루빅(Erno Rubik)이 발명해 1980년 특허를 받고 시판되면서 세계적인 인기를 끌었다. 건축학 전공으로 헝가리 공학아카데미 원장직에도 오른 루빅은 현재 계명대 건축학과 특임교수로 임명돼 강의를 펼치고 있다.

일반적으로 한 면 맞추기도 힘들지만 여섯면 모두를 맞추는 세계대회 신기록은 6.24초다. 호주의 16살 소년 펠릭스 젬덱스(Feliks Zemdegs)가 지난해 세웠다. 장난감 블록 ‘레고’로 만든 로봇이 세운 기록은 5.35초로, 국내산 스마트폰을 결합시켜 공간인식과 연산 기능을 해결했다. (동영상 참조 : http://youtu.be/_d0LfkIut2M)

큐브를 맞추다 보면 이런 질문이 떠오른다. “움직임을 최소화하면 몇 번만에 큐브를 맞출 수 있을까?” 수학적인 해법을 찾아낸다면 움직임을 줄여 세계기록을 단축시킬 수 있기 때문이다. 답을 찾는 과정에서 탄생한 것이 ‘신의 숫자(God's Number)’다. 더 이상 줄일 수 없는 최적의 숫자를 가리킨다.

1981년 52번의 움직임만으로 큐브를 맞춘 이래 ‘신의 숫자’를 찾아내려는 노력이 계속되어 왔다. 마침내 지난 2010년 7월에 4명의 과학자가 루빅스 큐브를 맞추는 ‘신의 숫자’가 20이라는 결론을 내렸다. 이들은 독특한 계산 알고리듬을 작성해서 35대의 컴퓨터로 시뮬레이션 프로그램을 가동시켰고, 4천325경 2천3조 2천744억 8천985만 6천개에 달하는 경우의 수를 모두 계산해냈다.

그런데 최근 격자를 이용한 비슷한 유형의 숫자퍼즐 ‘수도쿠(Sudoku)’에서도 신의 숫자가 발견돼 화제다. 이들은 54억개의 수도쿠 퍼즐을 분석해서 “최소한 17개의 힌트숫자가 주어져야 수도쿠를 풀 수 있다”는 결론을 얻었다. 계산 알고리듬을 밝힌 논문은 지난 1일 온라인 논문초고 등록사이트 ‘아카이브(ArXiv.org)’에 공개됐다. (링크 참조 : http://arxiv.org/abs/1201.0749)

루빅스 큐브의 ‘신의 숫자’는 20, 수도쿠는 17

‘수도쿠(Sudoku)’는 1979년 건축가 하워드 건스(Howard Garns)가 고안해내 ‘넘버 플레이스(Number Place)’라는 이름으로 최초 발표했다. 이후 1984년 일본의 퍼즐잡지가 ‘숫자는 한번만’이라는 의미로 수도쿠(數獨)라는 이름을 붙여 대중화시켰다.

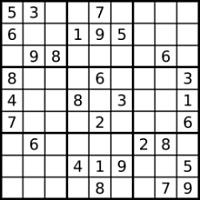
수도쿠 퍼즐의 규칙은 간단하다. 가로세로 9칸씩 총 81개의 칸에 1에서 9까지의 숫자 중 하나를 집어넣되, 가로 또는 세로줄을 이루는 각 9칸에 1에서 9까지의 숫자가 모두 하나씩만 들어가야 한다. 그리고 가로세로 3칸씩 총 9칸으로 이루어진 구획 안에도 1에서 9까지의 숫자가 모두 하나씩만 들어간다.

처음에는 어렵지만 몇 번 하다보면 숫자에 약한 사람이라도 쉽게 답을 찾을 수 있다. 수도쿠는 놀라운 중독성 덕분에 지능계발과 치매예방이라는 광고를 등에 업고 각국에서 선풍을 일으키고 있다.

수도쿠는 퍼즐 하나당 단 한 가지의 답이 존재해야 한다. 총 81개의 칸 여기저기에 고정된 숫자를 적어두면 정답의 가능성을 하나로 줄일 수 있다. 이들을 ‘힌트숫자(clue-number)’라 부른다. 힌트 숫자가 몇 개나 표시되어 있는지에 따라 초급, 중급, 고급으로 나뉜다.

수도쿠도 숫자를 이용한 퍼즐이기 때문에 루빅스 큐브 때와 비슷한 질문을 던질 수 있다. “힌트숫자를 최소한 몇 개나 표시해야 단 하나의 정답을 가진 수도쿠 퍼즐이 만들어질까?” 마찬가지로 수많은 수학자와 공학자들이 이 문제에 뛰어들었고 지금까지 밝혀진 개수는 ‘17’이었다. 81칸에 최소한 17개의 힌트 숫자가 표시되어야 퍼즐을 풀 수 있다는 것이다.

힌트숫자가 16개만 표기된 수도쿠 퍼즐은 존재할 수 없을까? 아직까지 명확한 계산식이 등장하지 않았기 때문에 가능성을 모두 계산해야만 증명이 가능하다. 호주의 수학자 고든 로일(Gordon Royle)을 비롯해 개리 맥과이어(Gary McGuire), 바스티안 투게만(Bastian Tugemann), 질 시바리오(Gilles Civario) 등 4명의 과학자가 지루하고 반복적인 증명과정에 뛰어들었다.

총 54억여개의 수도쿠 퍼즐을 일일이 검증

이들이 택한 방법은 단순하면서도 미련스럽다. 16개의 힌트숫자가 주어진 수도쿠 퍼즐을 모두 만들어서 일일이 성공여부를 검증하는 것이다. 그러나 이 방법을 실행하는 것은 말처럼 쉽지 않다.

수도쿠에 쓰이는 숫자는 1에서 9의 아홉개에 불과하지만, 경우의 수를 모두 곱해보면 엄청난 결과가 나온다. 자그마치 6,670,903,752,021,072,936,960개다. 우리말로 하면 66해 7천90경 3천752조 210억 7천293만 6천960개다. 1조의 66억배가 넘는 숫자다. 이 조합을 일일이 계산하려면 수백년도 모자란다.

맥과이어는 지난 2006년 이 문제에 뛰어들며 “수도쿠 퍼즐 하나를 1초 만에 검증하는 슈퍼컴퓨터가 있다 해도 모든 가능성을 점검하려면 173년이나 걸린다”고 밝힌 바 있다. 그는 “최근 기술로는 퍼즐 하나를 1분 정도에 계산할 수 있을 것”이라 예측하면서도 “이런 속도로는 컴퓨터 1만대를 연결해도 1년이 넘게 걸린다”고 설명하며 계산을 도와줄 알고리듬을 작성해 효율을 높여야 한다고 주장했다.

이후로 효율적인 알고리듬을 작성하기 위한 노력이 시작됐다. 반드시 들어가야 하는 ‘지표숫자’와 어떤 수를 넣어도 계산에 영향을 미치지 않는 ‘가변숫자’로 나누어 불필요한 부분을 제외하는 것이다.

수도쿠는 가로세로 3개씩 총 9칸으로 이루어진 구획, 그리고 이 구획이 9개 합쳐진 총 81칸의 전체 퍼즐로 구성된다. 가로세로 어느 방향으로 돌리든 구조는 바뀌지 않기 때문에 지표숫자와 가변숫자를 찾아낼 수 있다.

이렇게 하면 조합 가능한 경우의 수가 54억 7천273만 538개로 줄어든다. 이제부터는 일일이 검증하는 과정을 거친다. 논문의 공저자들은 아일랜드 하이엔드 컴퓨팅 센터(ICHEC)의 슈퍼컴퓨터 ‘스톡스(Stokes)’를 이용해 검증작업을 거쳤다. CPU 하나당 계산시간을 모두 합치면 710만 시간에 달하며 작업은 지난해 1월부터 12월까지 1년 동안 계속됐다.

54억여개의 퍼즐을 모두 분석한 결과, 16개의 힌트숫자만으로는 단 하나의 해답을 가진 수도쿠 퍼즐이 만들어질 수 없었다. 최소한 17개의 힌트숫자가 있어야 하므로 수도쿠를 푸는 ‘신의 숫자’는 17이라는 사실을 증명한 셈이다.

맥과이어는 “논문에 쓰인 방법은 슈퍼컴퓨터를 이용해 무차별 공격(brute force)을 가하는 방식”이라며 “뛰어난 수학자가 더 우아한 알고리듬을 만들어 다시 증명하기 바란다”고 논평했다.